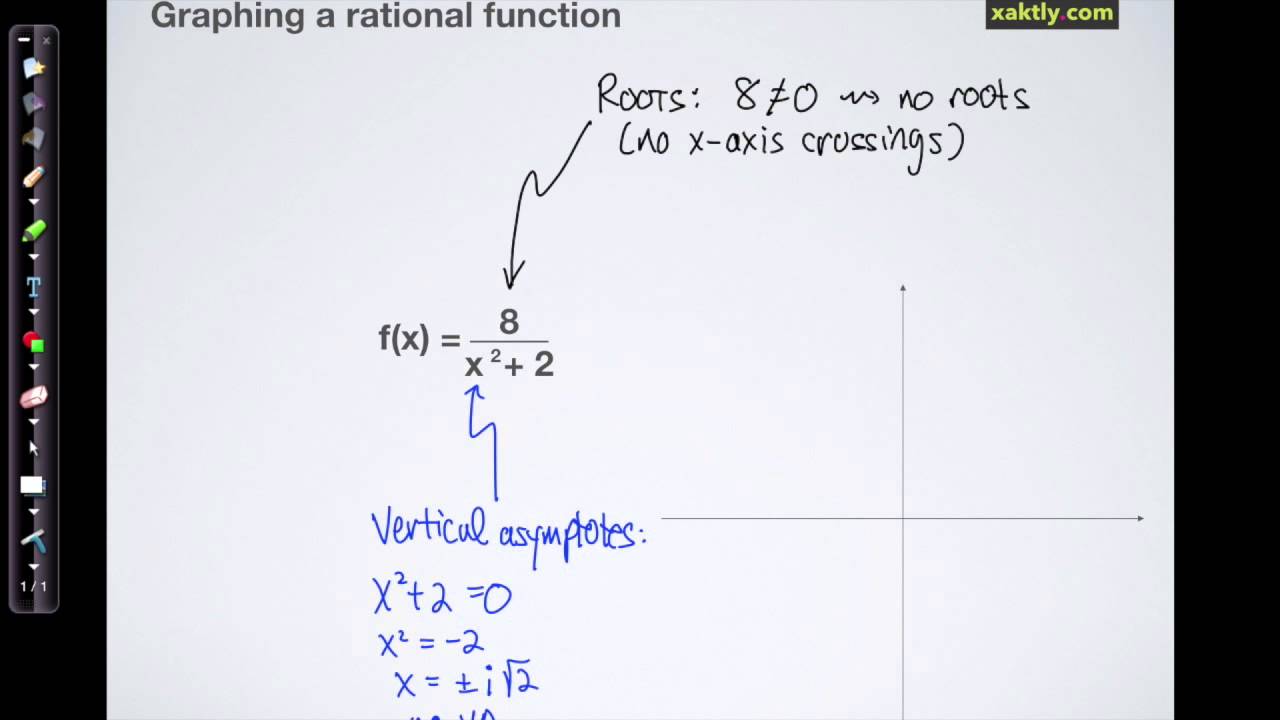
Use the graph of a function to graph its inverse Now that we can find the inverse of a function, we will explore the graphs of functions and their inverses Let us return to the quadratic function \displaystyle \left 0,\infty \right) 0, ∞), on which this function is onetoone, and graph it as in Figure 7 Figure 7 · f(x) = { (xa, x < 2), (4, x = 2), (xb, x > 2) } where a,b are constants For x < 2 we have f'(x)=1 => f(x)=xa, ie a straight line with gradient 1 For x > 2 we have f'(x)=1 => f(x)=xb, ie a straight line with gradient 1 We want f(2)=4 and we are not told anything about the gradient when x=2 (and in fact f'(2) will be undefined) and we are not told that that the functionGraph f (x)=1/x f (x) = 1 x f ( x) = 1 x Find where the expression 1 x 1 x is undefined x = 0 x = 0 Consider the rational function R(x) = axn bxm R ( x) = a x n b x m where n n is the degree of the numerator and m m is the degree of the denominator 1
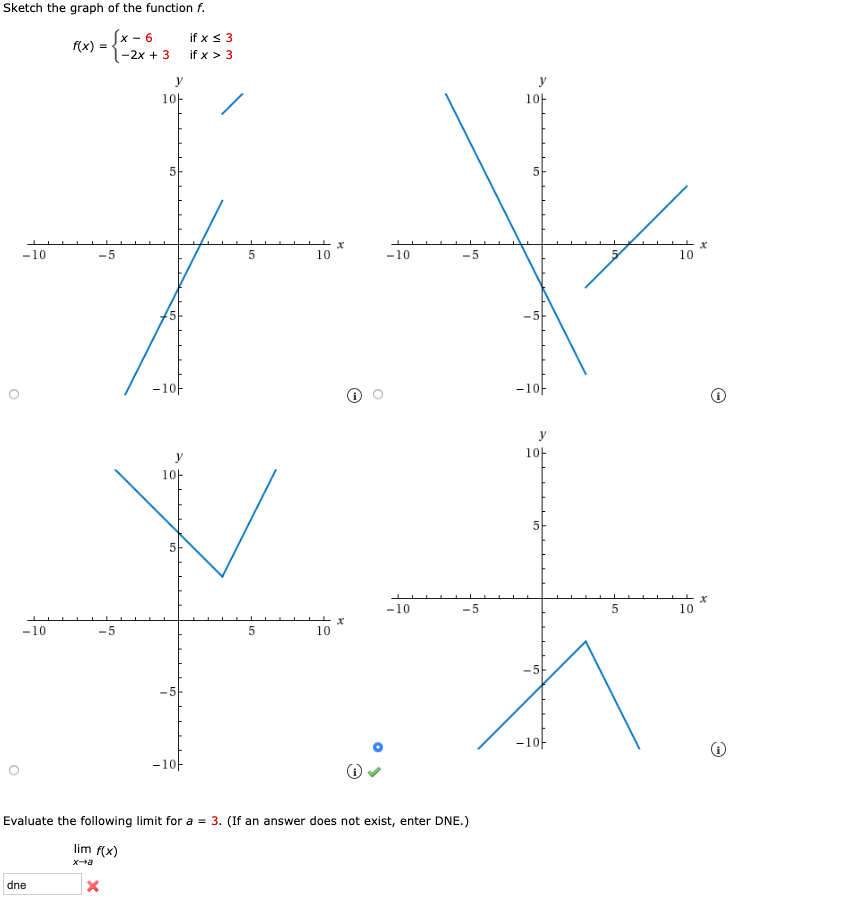
Answered Sketch The Graph Of The Function F X Bartleby
Sketch the graph of the function. f(x y) = 11 − 4x − 5y
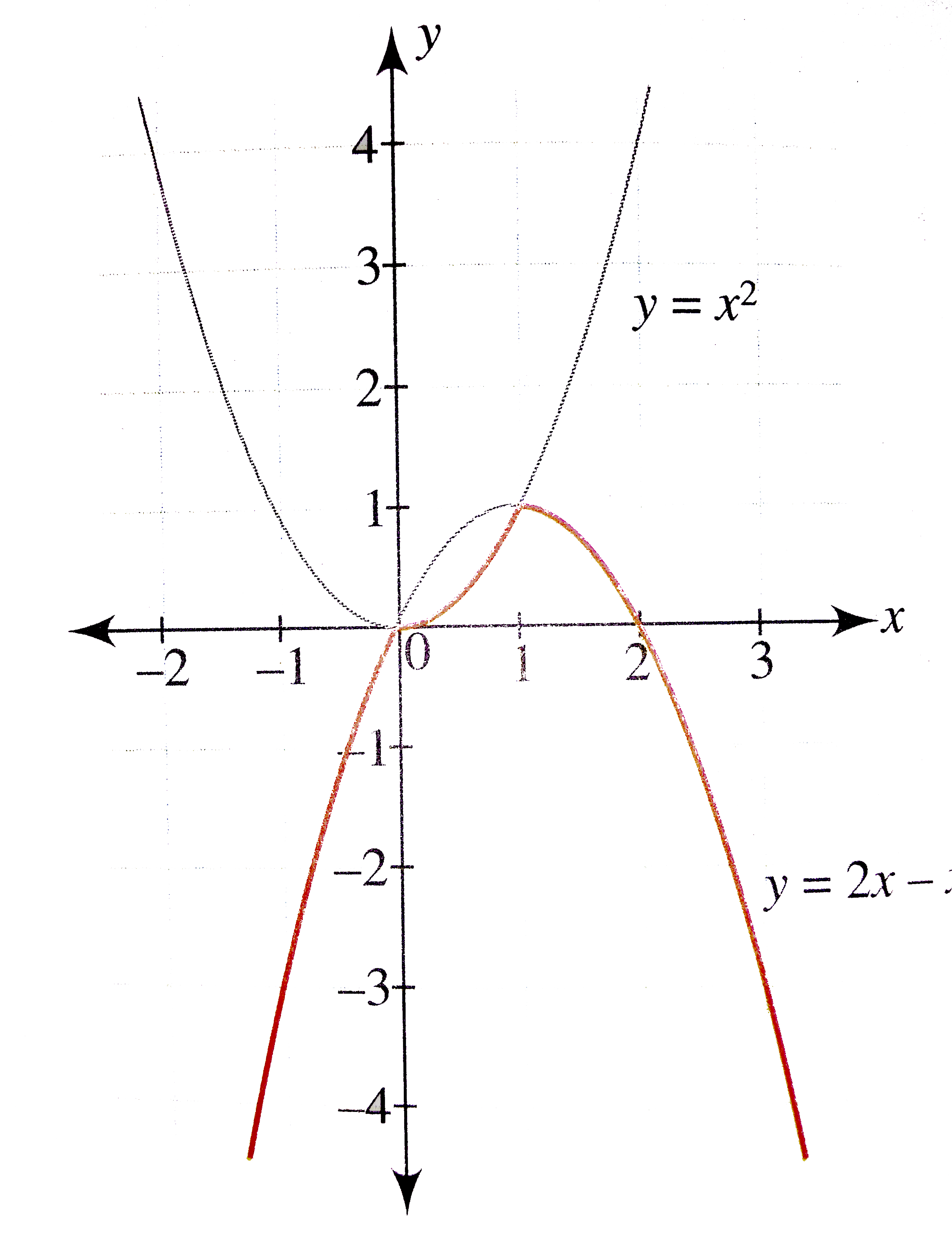
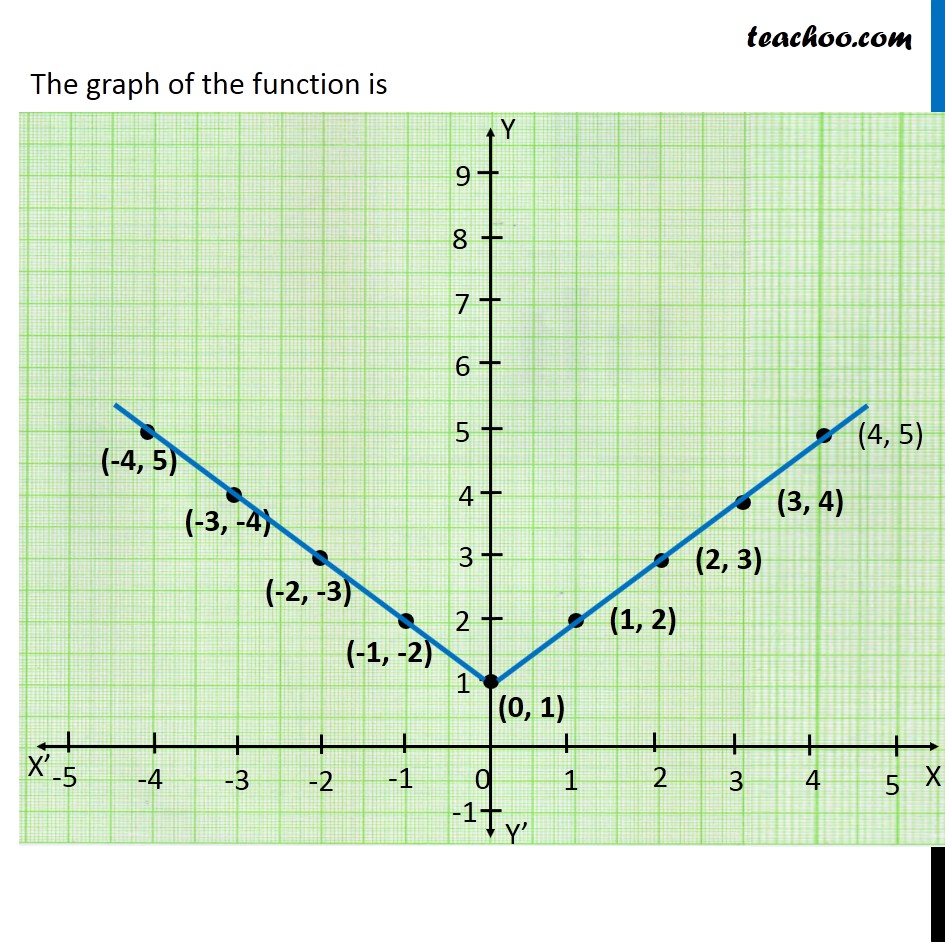
Sketch the graph of the function. f(x y) = 11 − 4x − 5y-0309 · Drawing graphs of y=1/f(x) and y=I1/f(x)I from y=f(x) Discover Resources Transformations of Cosine;2801 · Example 14 Draw the graph of the function f R → R defined by f (x) = x3, x ∈ R f (x) = x3, x ∈ R Also, f R → R We find various values of f (x) by using different values of x Domain is a real number Range is a Real number The graph of the function is




Example 22 Function F Is Defined By F X 1 X 1 X 1
Graph f (x)=xe^ (x) f (x) = xe−x f ( x) = x e x Find where the expression xe−x x e x is undefined The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined The vertical asymptotes occur at areas of infinite discontinuityI got that the VA of the new grFor part C, we have F f X minus two that will make the graph slide or shift to to the right So take every coordinate and just move it to to the right, the Schapelle of the same It will just slide next one Now we're changing that so that the graph has that minus two outside, and that's going to affect the graph vertically
This is a typical test problem in algebra classes, specifically college algebra · To sketch y = 1/f(x) This should be obvious but note that the sign of f(x) is the same sign as 1/f(x) So for a given domain, no part of the graph of f(x) should suddenly switch to the other side of the xaxis when graphing 1/f(x) The function is undefined when f(x) = 0The limit of the function is executions One from the positive side equals and finish Let's mark this one in red In order to graph this limit, you look at X equals one and then we see that as X approaches one from the positive side, the Y value will approaching finicky So it'LL look something like this not actually touching one
Sketch the graph of a function y = f ( x) with all of the following properties a f ′ ( x) > 0 for − 2 ≤ x < 1 b f ′ ( 2) = 0 c f ′ ( x) > 0 for x > 2 d f ( 2) = 2 and f ( 0) = 1 e lim x → − ∞ f ( x) = 0 and lim x → ∞ f ( x) = ∞ f f ′ ( 1) does not exist1217 · Since the derivative is greater than 0 on all x excluding x = 2, we know the function is increasing until it gets to x= 2, where it plateaus, and then it starts increasing again A perfect example of this would be the cubic function f(x) = (x 2)^3 1, as pictured in the following graph Hopefully this helps!1 7 if x = 1 x2 1 if x >




Answered Sketch The Graph Of The Function F X Bartleby
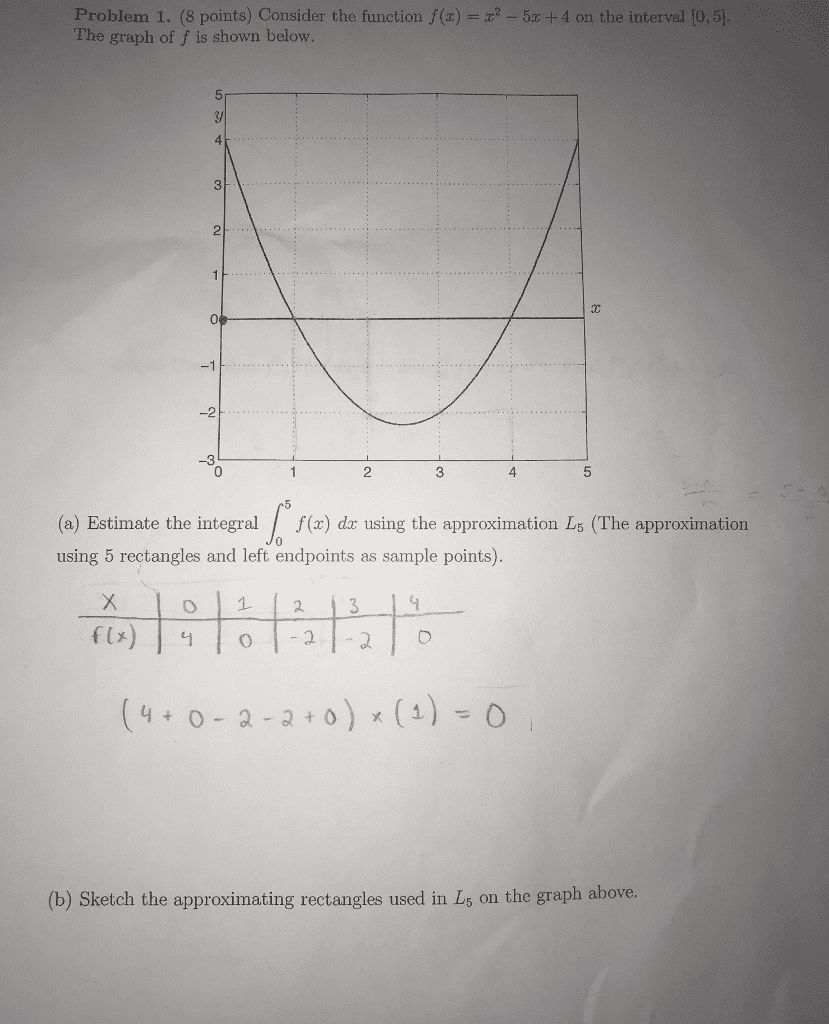



Oneclass Consider The Function F X X2 5x 4 On The Interval 0 5 The Graph Of F Is Shown Below A
F (x 2) = F (x) (a) Sketch The Graph Of The Given Function For Three Periods (b) Find The Fourier Series For The Given Function F (x) = 1 2 ∞ K = 1Graph of the Function Sketch a graph of \(f\left( x \right)\) using all the information obtained above Further we use this algorithm for the investigation of functions Solved Problems Click or tap a problem to see the solution Sketch graphs of the following functions (Examples \({123}\))4 5 This is the graph of the given piecewise defined equation Interpretation The part of the graph to the left of x = 2 coincides with the graph of f ( x) = 1 − x 2 and the part of the graph to the right of x = 2 coincides with the graph of f ( x) = x The open dot at ( 2, 2) indicates that this point is excluded from the graph arrow_back



Solved 5 Details Scalcet8 4 Sketch The Graph Of A Function That Satisfies All Of The Given Conditions F X Gt 0 For All X 1 Vertical Asymp Course Hero
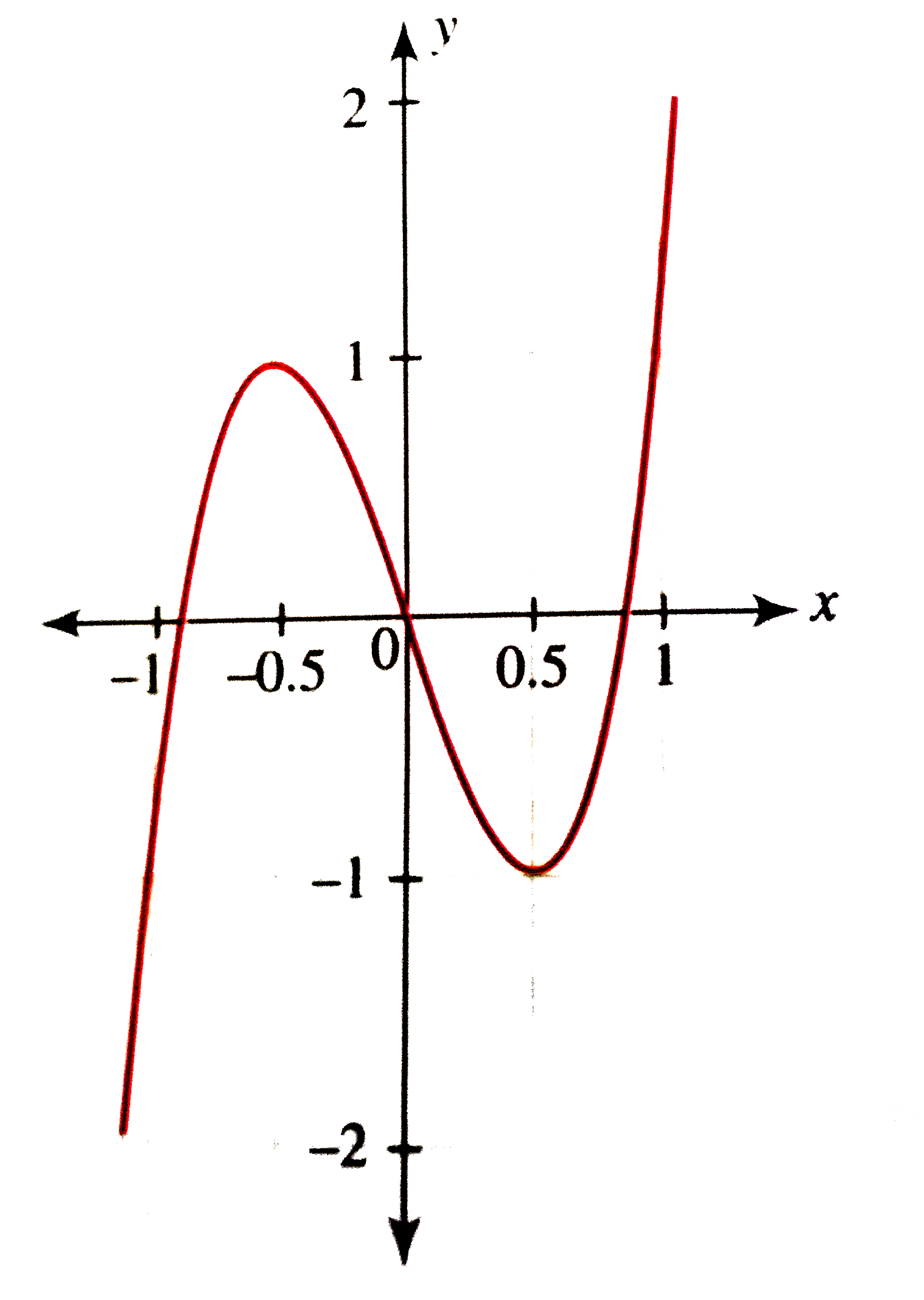



Draw The Graph Of F X 4x 3 3x And Hence Draw The Graph Of G
How to look at the different behavior of f(x) to sketch an accurate graph of f'(x) · Question Consider The Following F (x) = X 1, −1 ≤ X < 0, 1 − X, 0 ≤ X < 1; · Graph transformations Given the graph of a common function, (such as a simple polynomial, quadratic or trig function) you should be able to draw the graph of its related function




Sketch The Graph Of The Following Function F X X 1 D




Help Needed With Calculus Question Wyzant Ask An Expert
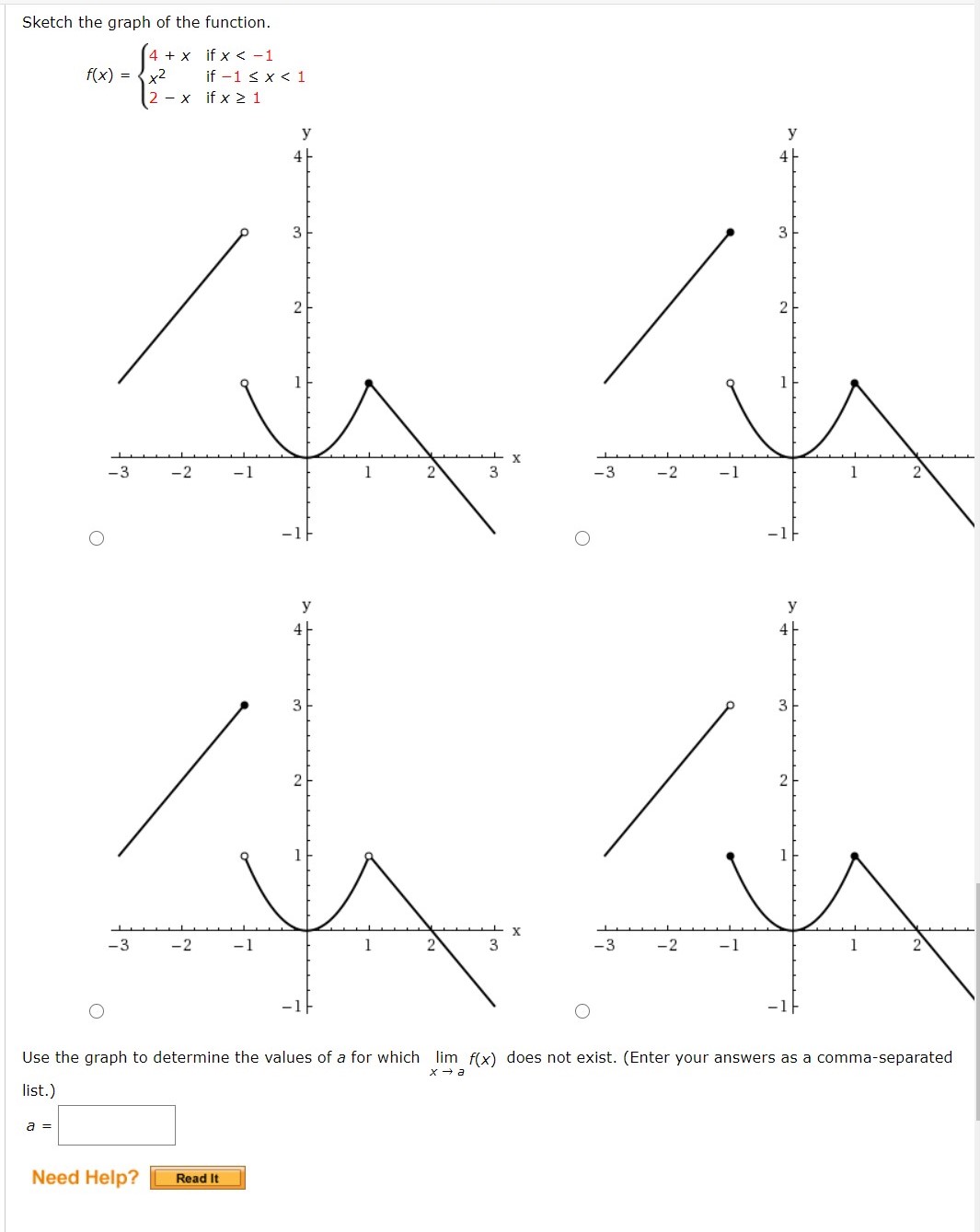
Sketch the graph of y = g(x) by starting with the graph of y = f(x) and using transformations Track at least three points through the transformations State the domain and range of gUse The Graph To Determine The Values Of A For Which Lim X → A F (x) Does Not Exist (Enter Your Answers As A Commaseparated List)Linear functions have the form f(x) = ax b, where a and b are constants In Figure 111, we see examples of linear functions when a is positive, negative, and zero Note that if a > 0, the graph of the line rises as x increases In other words, f(x) = ax b is increasing on ( − ∞, ∞)
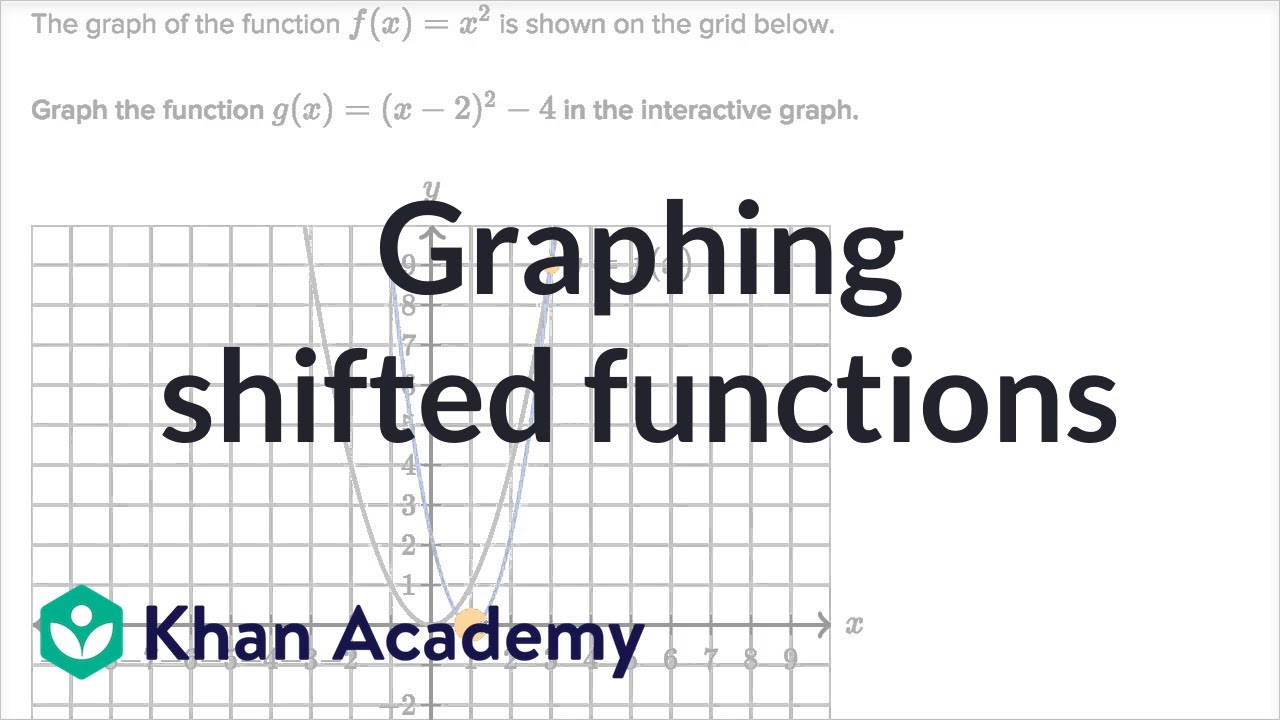



Graphing Shifted Functions Video Khan Academy
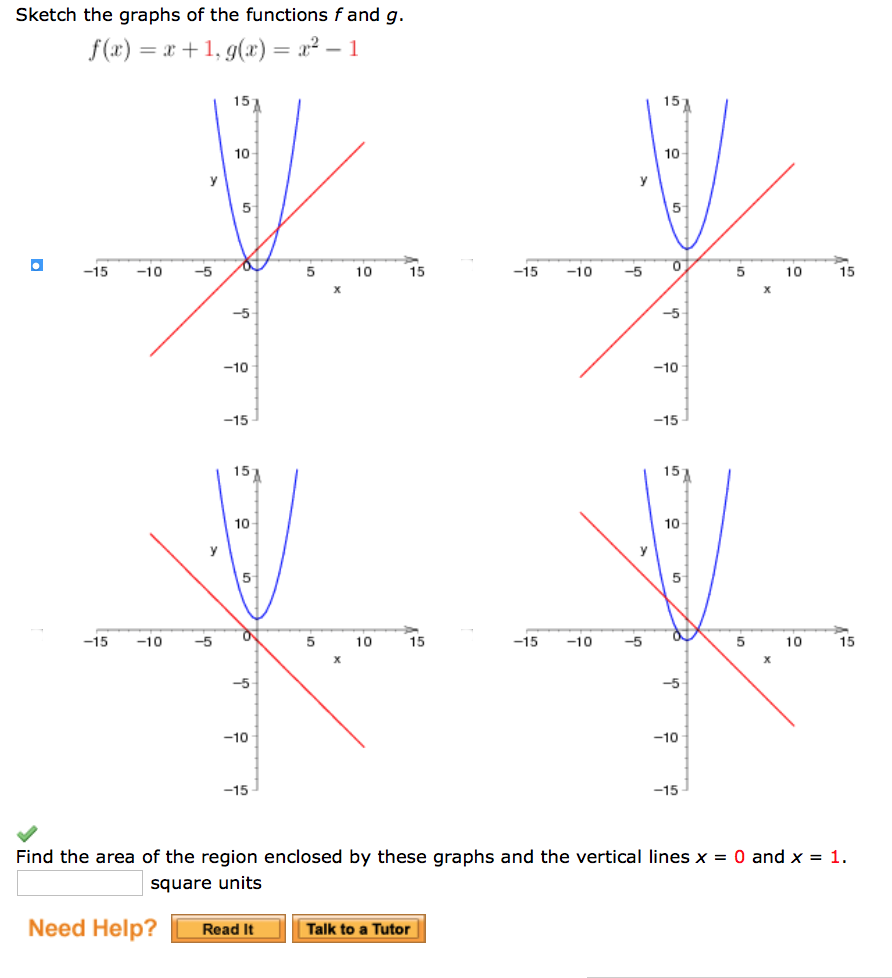



Solved Sketch The Graphs Of The Functions F And G F X Chegg Com
About "How to Sketch a Graph of a Function With Limits" How to Sketch a Graph of a Function With Limits Here we are going to see h ow to sketch a graph of a function with limits Question 1 Sketch the graph of a function f that satisfies the given values f(0) is undefined lim x > 0 f(xAnswer to Sketch the graph of the following function h(x) = x^{\frac{1}{3}} (x4) Indicate all important points By signing up, you'll getMore_vert Find the domain and sketch the graph of the function f ( x ) = x 2 if x <



What Is The Horizontal Line Test Expii



How Do You Graph Y 1 X 1 Socratic
Functions & Graphing Calculator \square!1215 · Sketch the graph of an example of a function f(x) that satisfies all of the following conditions Here is what I have so far Am I on the right track?Graph of f 1 Sketch the graphs of the inverse functions for y = p 4x 4 and y = x3 1 using the graphs of the functions themselves shown on the left and right below respectively To sketch a graph of the inverse function you must draw the mirror image of the graph of the function itself in the line y = x



Relations Graphs And Functions




Example 22 The Function F Is Defined By F X Left Begin Array L L 1 X X 0 End Array Right Draw The Graph Of F X
For the graph such that the function is $ y = \frac{ax}{bcx} $ where a = 2, b = 1 and c = 1/2 how do you sketch the graph of $ y = \frac{bcx}{ax} $ ??If f is odd, you see only one graph Example 6 Graph f(x) = (x 2)^2 and g(x) = f(x) Because you see two distinct graphs, f is not odd Now enter f(x) = x*(x^2 1) and "turn off" the graph of g by unchecking the box to the right of the text box and click Graph again With this function f, the graph of g is the same as the graph of fSketch the graph of one function that satisfies ALL of the following conditions (Many correct answers are possible) f(0) = 0
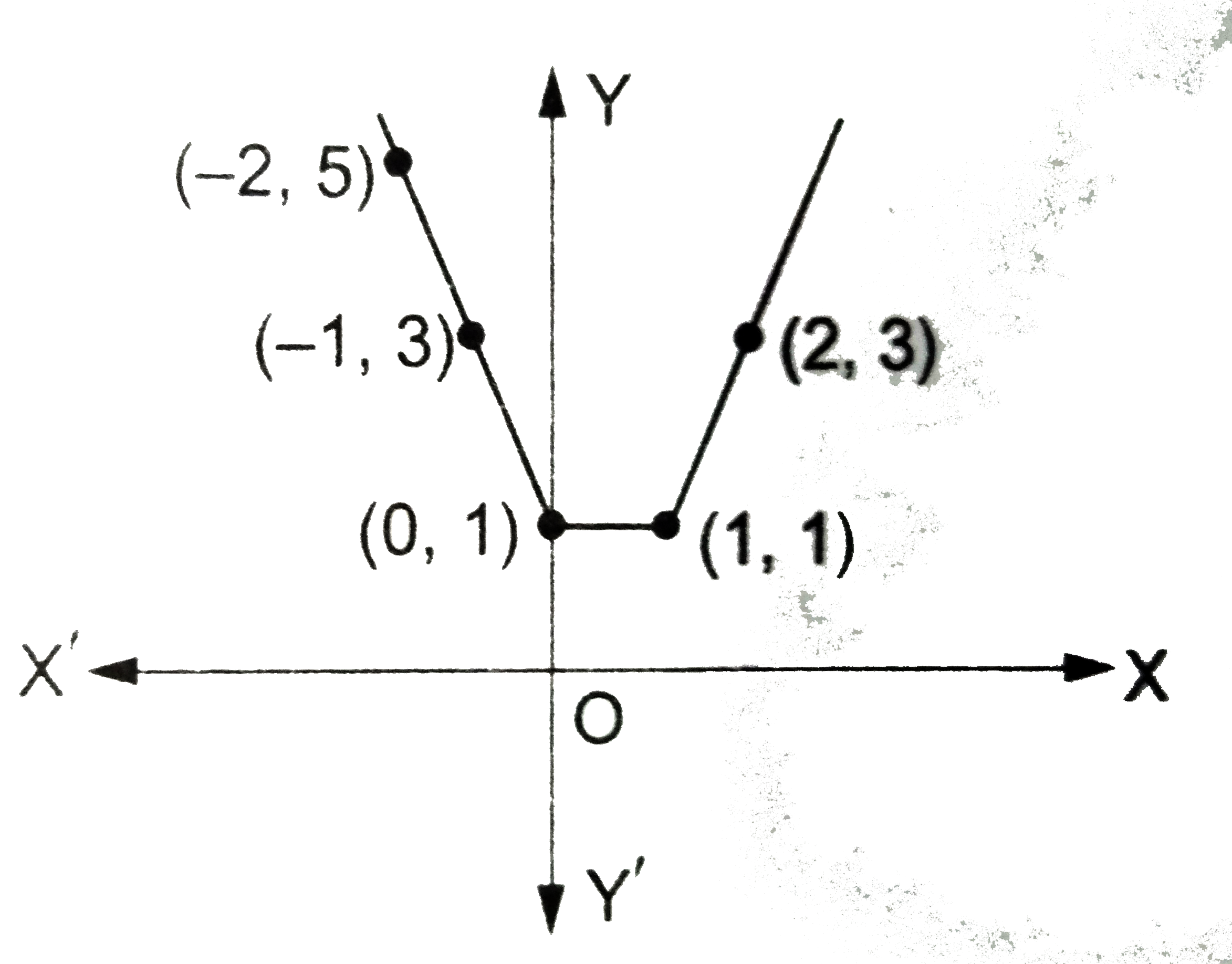



Draw The Graph Of The Function F X X X 1
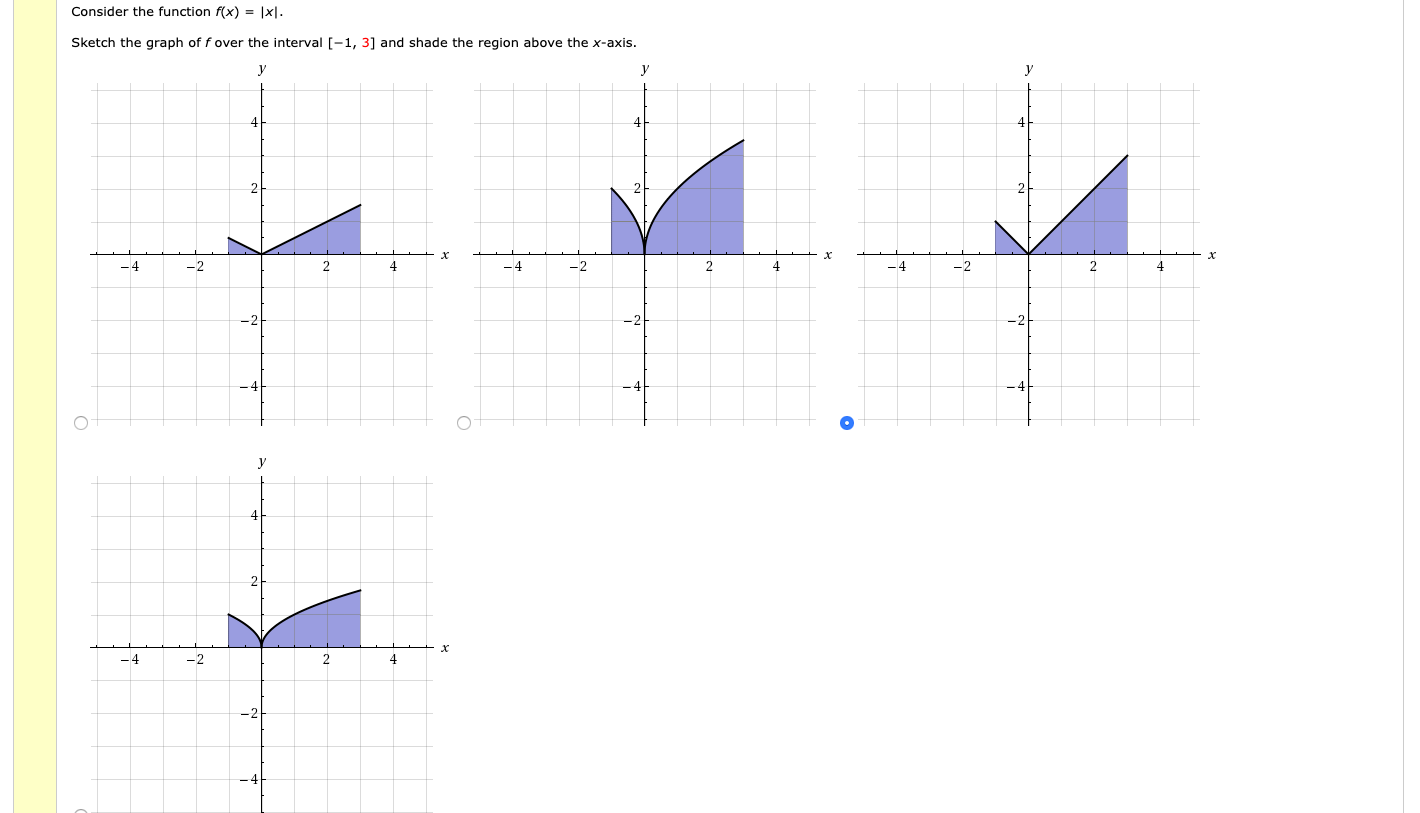



Consider The Function F X X Sketch The Graph Of Chegg Com
· Using the inbuilt graphing tool we get graph as shown in figure above It is an exponential graph We note that at x=0, f(x)=e^x1 becomes f(0)=e^01=2 For large ve values of x, function approaches oo exponentially For ve values of x, function approaches 1The function is decreasing all the way to the turning point, but another key is the change in concavity at just before x=1 This is a suspiciouslooking function to me almost certainly likely to be piecewise when f is multiplied by x, the zeros remain unchanged The left half of your original (for xSketch the graph of a continuous function f that satisfies the following conditions f(0) = 4 f(3) = f(3) = 0 f'(3) = 0 f'(0) does not exist f'(x) > 0 when 3 < x < 0




Function Tables Desmos




Finding The Derivative Of A Function Looking At A Graph Mathematics Stack Exchange
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!1 Evaluate given a = 1 (If an answer does not exist, enter DNE) lim x→a f(x) This question hasn't been solved yet Ask an expert Ask an expert Ask an expert done loading Sketch the graph ofClick here👆to get an answer to your question ️ \"Sketch the graph of the function \\( f ( x ) = x 1 \\)\"



Answered Sketch The Graph Of The Function 4 X Bartleby
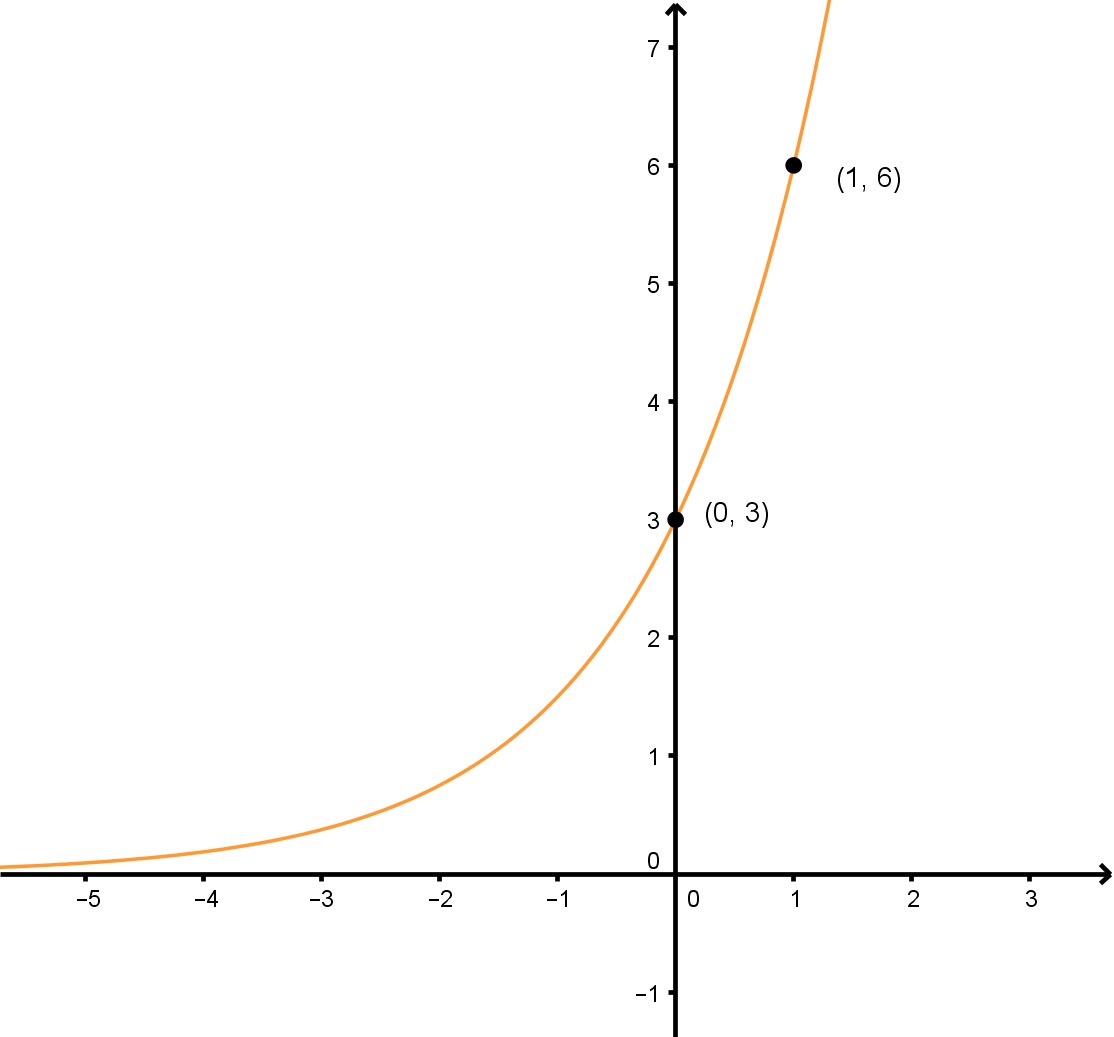



How To Find Equations For Exponential Functions Studypug
Question Sketch the graph of the function f f(x) = −5x 7 if x <Sketch the graph of the function f(x, y) = x^2 4y^2 1 Join our free STEM summer bootcamps taught by experts Space is limitedGeometry by Mazin kalil;



Polynomial Functions




Sketch Graph Of The Function From Given Conditions Youtube
0 1 − x if x ≥ 0Question A Sketch The Graph Of The Following Function F (x) = −e (1/4)x B Find The Area Of The Region Bounded Below By The Graph Of F And Above By The Xaxis From X = −4 To XView Tutorial 10pdf from MATH 002 at Swinburne University of Technology Tutorial 10 1 Sketch the graph of the following function (a) f ( x ) = x 2 , −π ≤ x ≤ π f= ( x ) f ( x 2π )




Example 22 Function F Is Defined By F X 1 X 1 X 1




Solved Sketch The Graph Of The Function F X 4x 1 3 Chegg Com
Functions on the Real Line Overview In mathematics, a function (or map) f from a set X to a set Y is a rule which assigns to each element x of X a unique element y of Y, the value of f at x, such that the following conditions are met 1) For every x in X there is exactly one y in Y, the value of f at x;Analyze and sketch graph of the function {eq}\displaystyle f(x)=\frac{2x}{1x^2}{/eq} Label any intercepts, relative extrema, points of inflection, and asymptotes Use a graphing utility toSketch the general shape of the graph of f(x) given the gradient function shcwn at right I Determine the general ehape of the graph of ax) by raising the degree off'(x) by one 2 Locate the turning points, ie the xintercepts (Turning points occur when f'(x) = O) 3 the magnitude and betwviour of the gradients 4 Sketch the general



Answer In Calculus For Desmond



Draw The Graph Of The Function F X X X X 2 1 Le X Le 1
Answer to Sketch the graph of a function that satisfies all of the given conditions a f (0) = f (4) = 0 b f (x) = 1 if x 1 c f (x) 0Look below to see them all They are mostly standard functions written as you might expect You can also use "pi" and "e" as their respective constants Please note You should not use fractional exponents For example, don't type "x^(1/3)" to compute the cube root of x Instead, use "root(x2) If x and y are in X, then f (x) = y



Answered Consider The Following X 1 F X 5x Bartleby




3 Ways To Graph A Function Wikihow
· Calculate derivative f'(x) = 3 x^2 6 x = 3x (x2) So you can study the sign of f'(x) f'(x) < 0 iff x in 0,2 f'(x) > 0 iff x in oo, 0 cup 2,oo You get now the variations of f f is decreasing on 0,2 f is creasing on oo, 0 and on 2,oo Remark that f has local maximum in 0 with f(0)=0 local minimum in 2 with f(2) =4 There are two horizontal tangents at 0 and atI think the graph satisfies all of the conditions, but the lines cross at about (2,3) is that acceptable?Question Sketch The Graph Of The Function F (x) = 3 X If X < −2 X2 If −2 ≤ X < 2 6 − X If X ≥ 2 *The Lower Left Hand Graph Is The Correct Graph!




Draw The Graph Of The Function F R Gt R Defined By F X X 3 X In R Youtube




Draw The Graph Of The Function F X X 1 Brainly In
From the graph, the minimum value occurs x = 1 and is estimated as f ( 1) = e Use derivative concept to explain these features y = x e 1 x is not defined at x = 0 , take − 1 x 1 = 0 and solve for x Therefore, the local minimum occurs x = 1 and is the minimum value is f ( 1) = e Observe that not possible values for x if f " ( x) = 0Section 35 Curve Sketching We have been learning how we can understand the behavior of a function based on its first and second derivatives While we have been treating the properties of a function separately (increasing and decreasing, concave up and concave down, etc), we combine them here to produce an accurate graph of the function without plotting lots of extraneous pointsAnswer to (a) Sketch the graph of the function f(x) = x 2 − 3x 4 on the interval −3 ≤ x ≤ 5 What is the maximum value o



A Sketch The Graph Of F X 3x Ppt Download
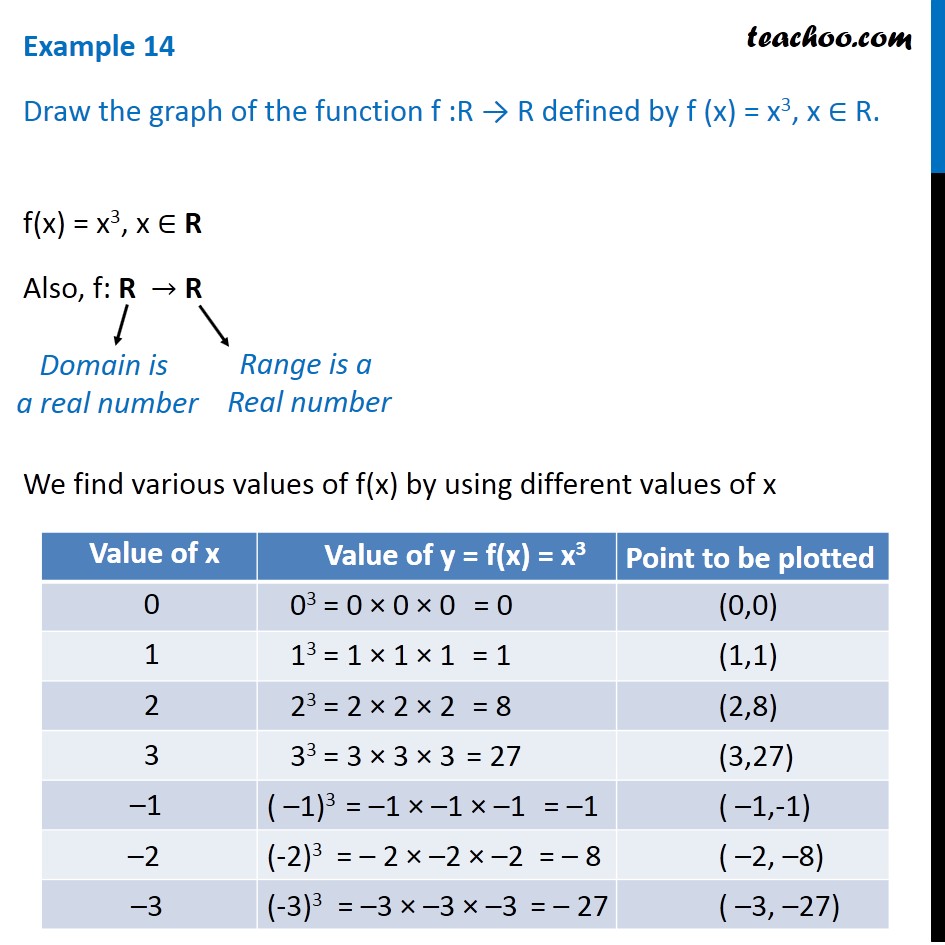



Example 14 Draw Graph Of F X X 3 Chapter 2 Class 11
· See sample drawing in explanation below Example curve f(x) = x^33x^29x2 Sketching the graph is fairly straightforward once you interpret what each piece of the problem tells you about the shape of the graph f'(x)>0 when 1 < x < 3 The first derivative tells you whether the graph is increasing ("going upwards") or decreasing ("going downwards")Sketch the graph of f(x)=x/(x^21) using its domain, symmetry, intercepts, asymptotes, relative extrema, and any points of inflection Identify the open int




Given The Graph Of F X Sketch The Graph Of The Following Function Transformations On The Same Brainly Com
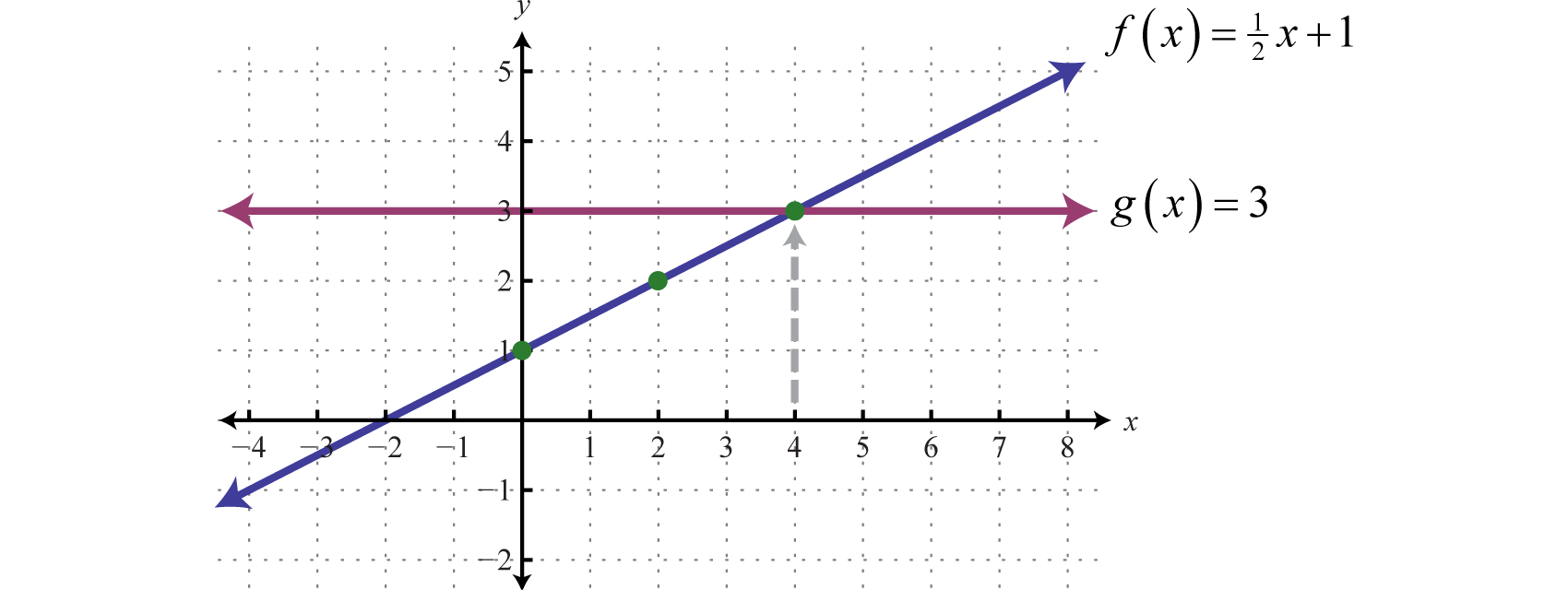



Linear Functions And Their Graphs




Sketch The Graph Of The Function F X 2 X 1 3 Using Transformations Do Not Plainmath




Here Are Graphs Of Two Functions F And G The Function H Is Defined By H X F X G X 1 For Which Brainly Com




Extension 1 Functions Worksheet By Ezymathtutoring Issuu




Math 157 Limit Continuity Differentiability Exercise Set 1 Function Mathematics Derivative
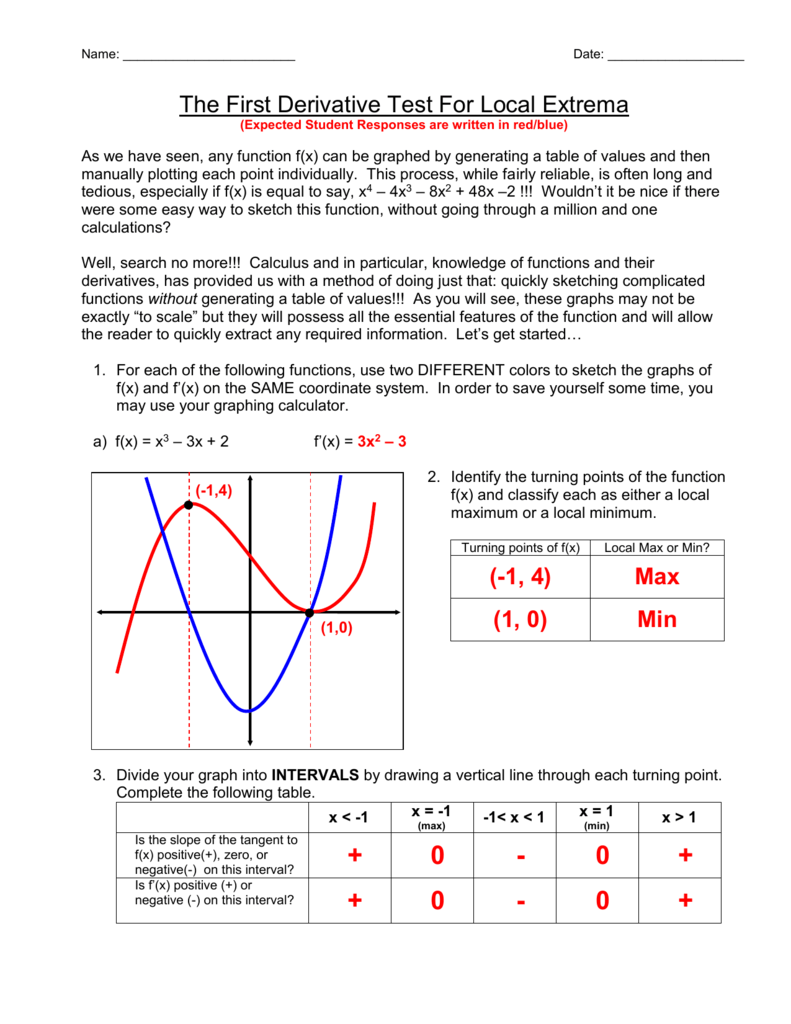



The Slope Of The Tangent To F X



Answer In Calculus For Moreen




Horizontal Line Test For Function To Have Inverse Expii



Solved The Graph Of Y I 4x X2 Is Given Use Transformations To Create A Function Whose Graph Is As Shown Course Hero
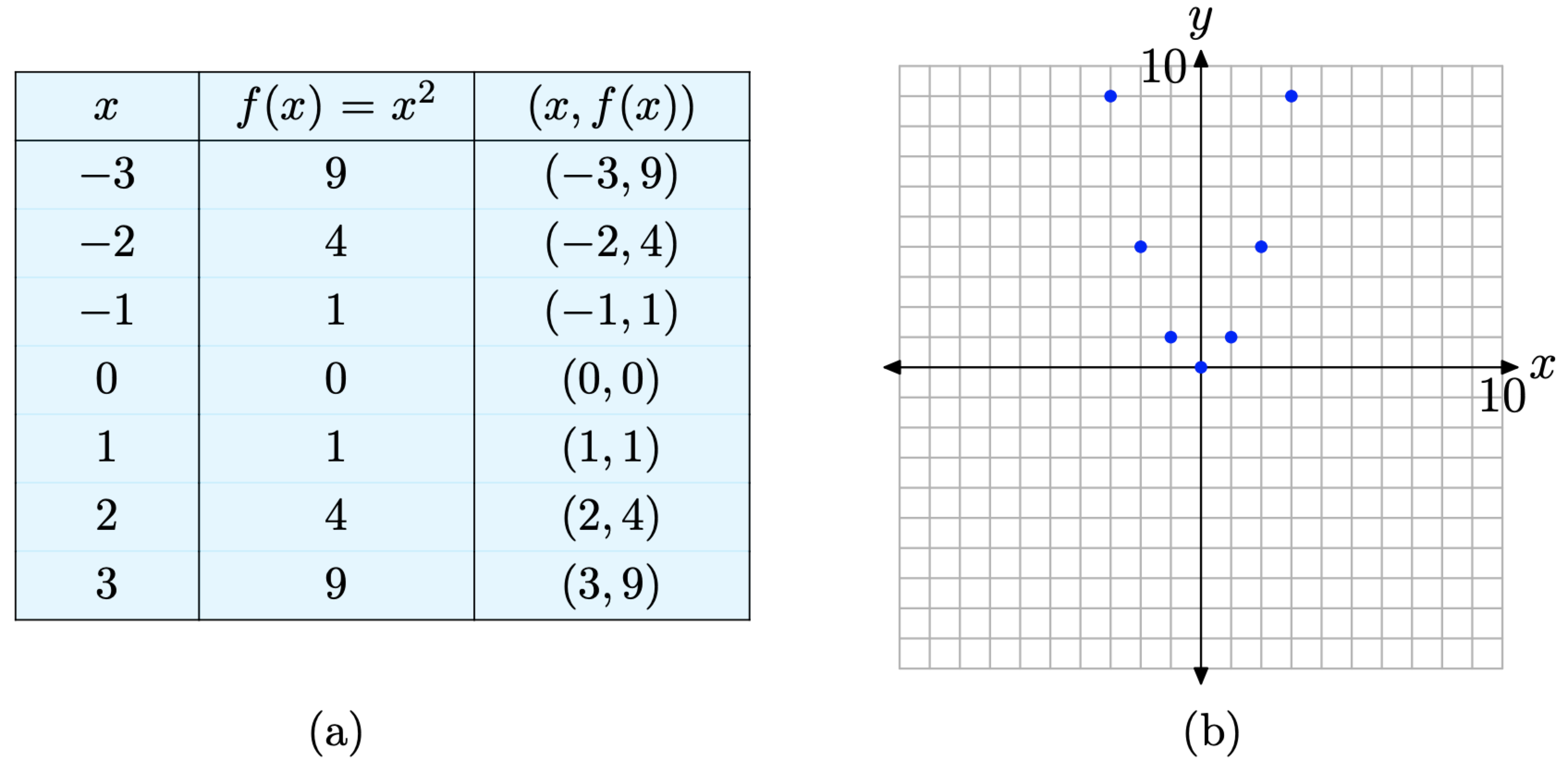



2 2 The Graph Of A Function Mathematics Libretexts
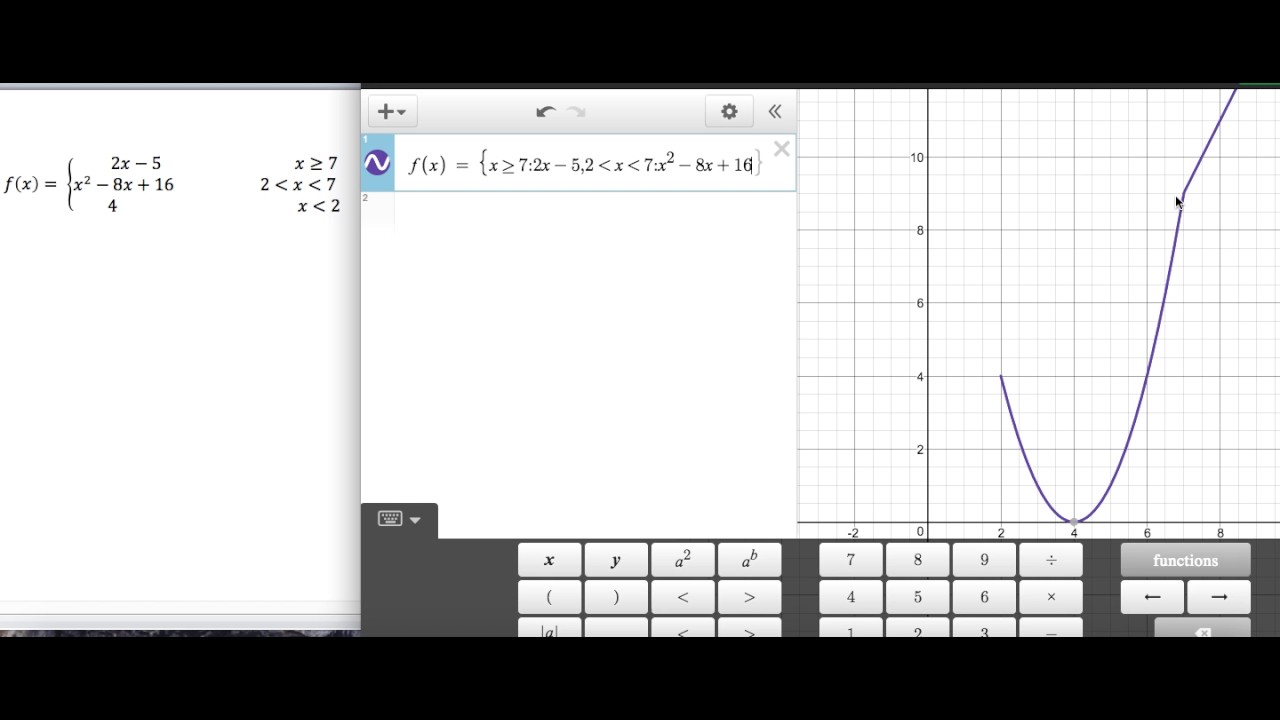



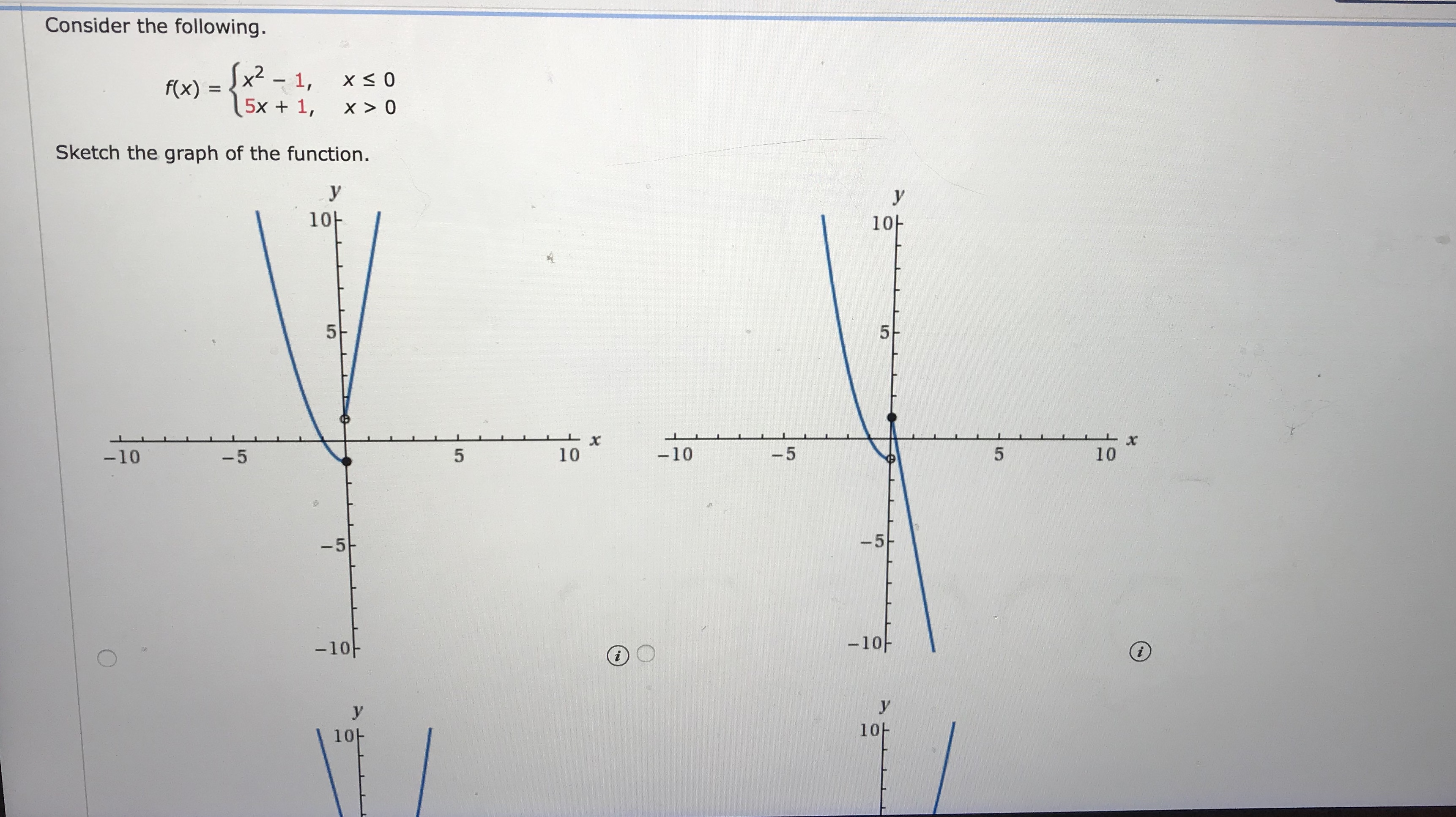
Piecewise Defined Functions College Algebra



Example 22 Function F Is Defined By F X 1 X 1 X 1
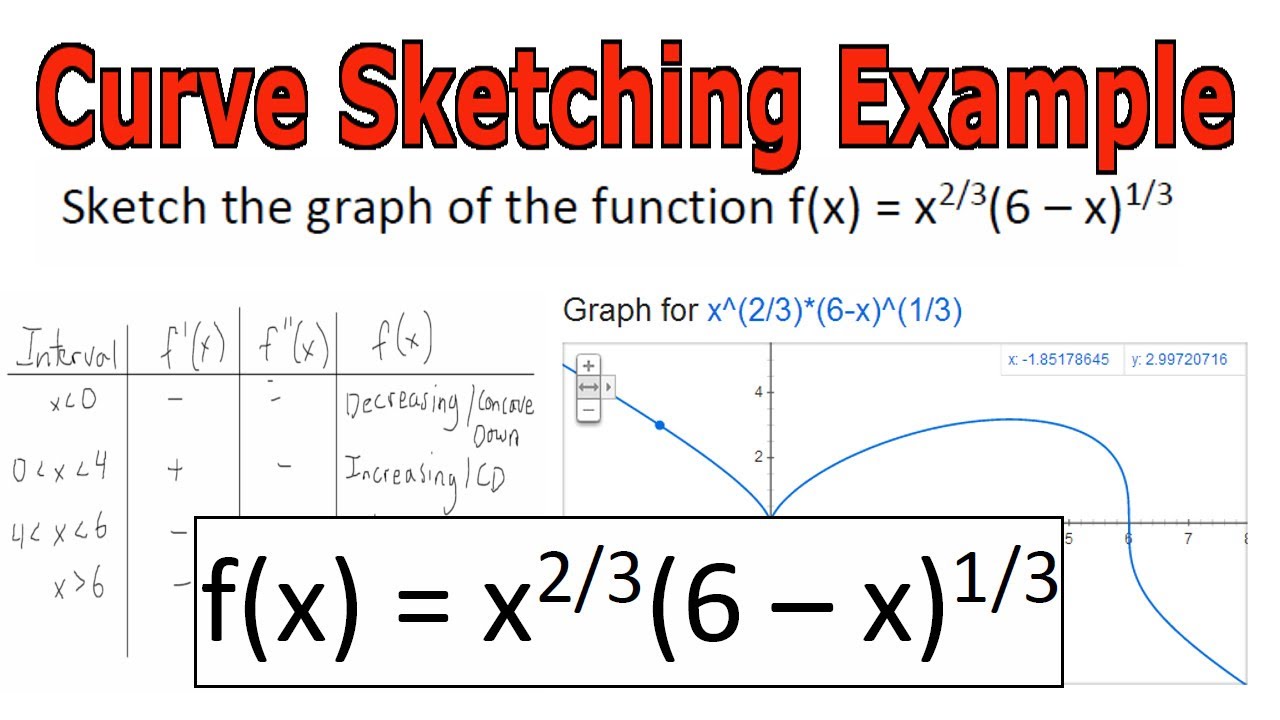



Curve Sketching Example Y X 2 3 6 X 1 3 Youtube




Using Transformations To Graph Functions




Rational Functions




A Sketch The Graph Of F X 3x Ppt Download
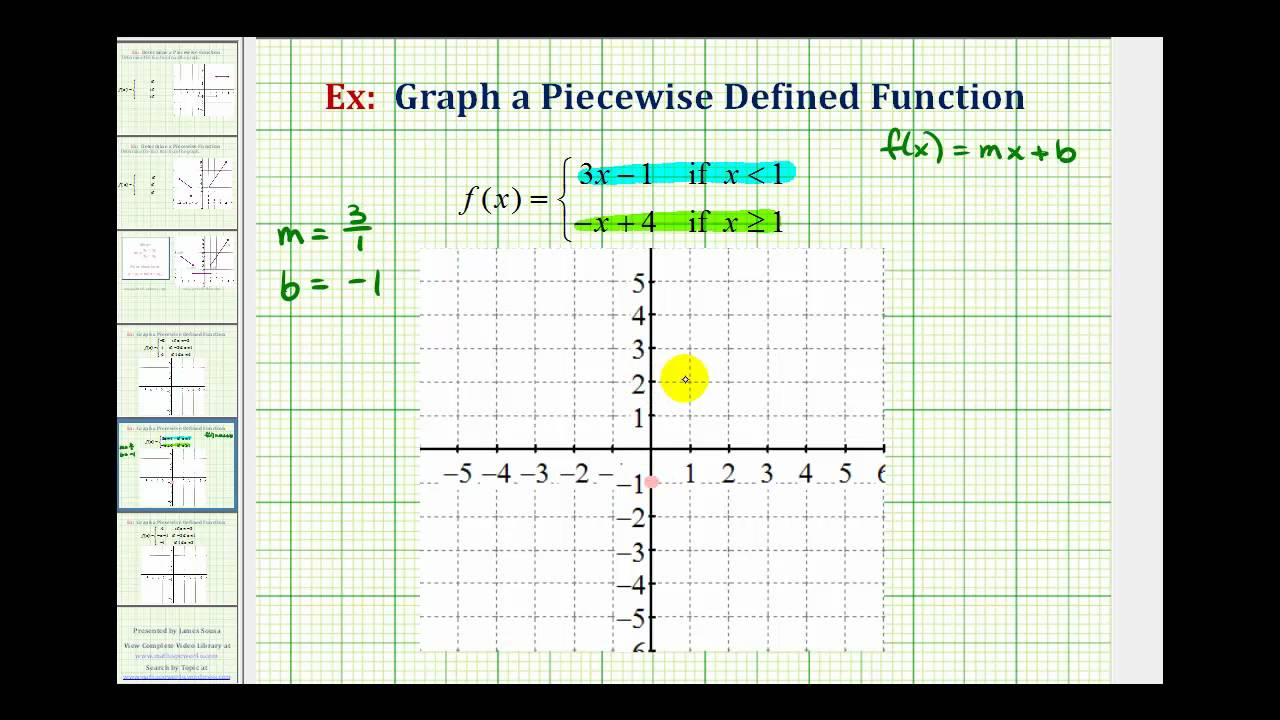



Graph Piecewise Defined Functions College Algebra




12 Draw The Graph Of Real Function F X 1 X 2



How Do You Determine Whether The Function F X Ln X 2 7 Is Concave Up Or Concave Down And Its Intervals Socratic




Reflecting Functions Examples Video Khan Academy
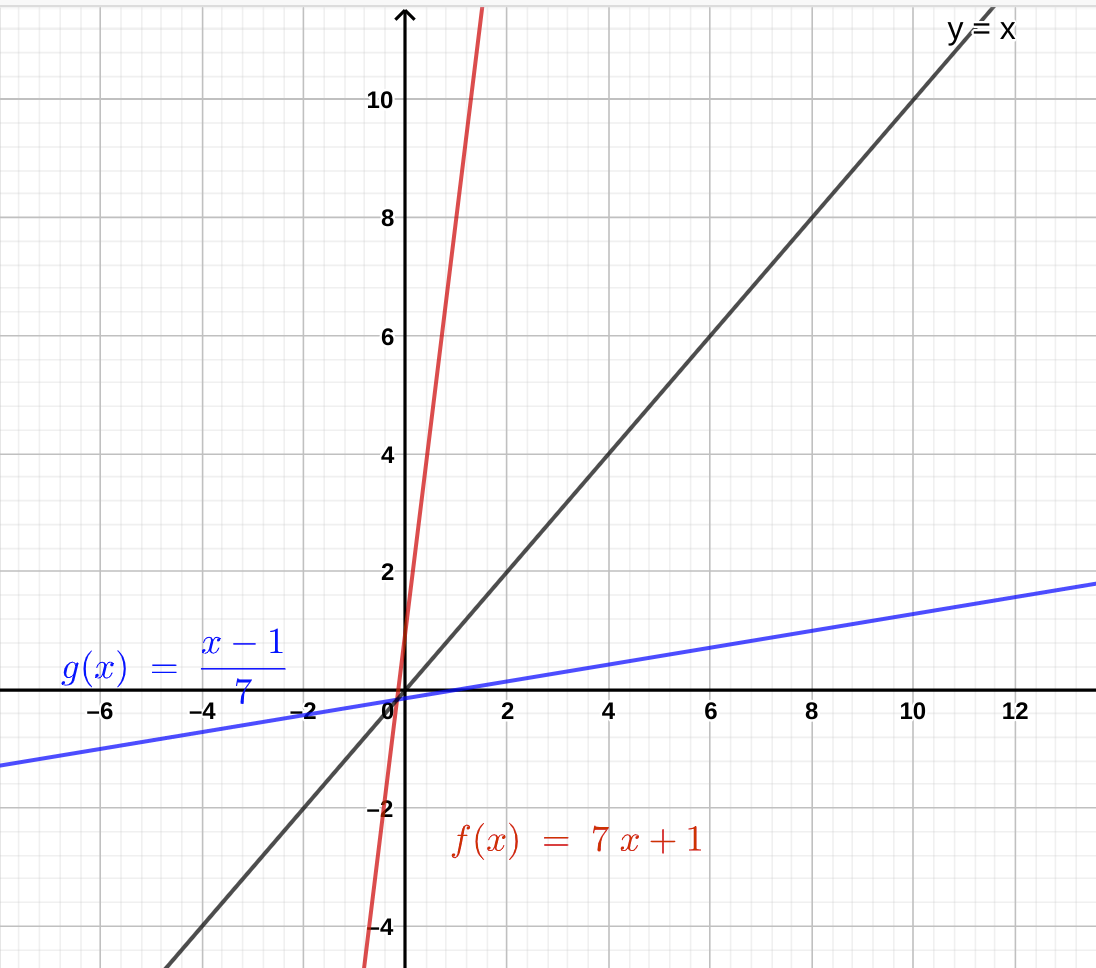



Sketch The Graphs Of The Inverse Functions In The Same Coordinate Plane And Show That The Graphs Are Reflections Of Each Other In The Line Y X Math F X 7 X 1 Quad F 1 X Frac X 1 7 Math Homework



Ap Calculus Ab Multiple Choice 1998 Exam Part B Videos Questions Solutions
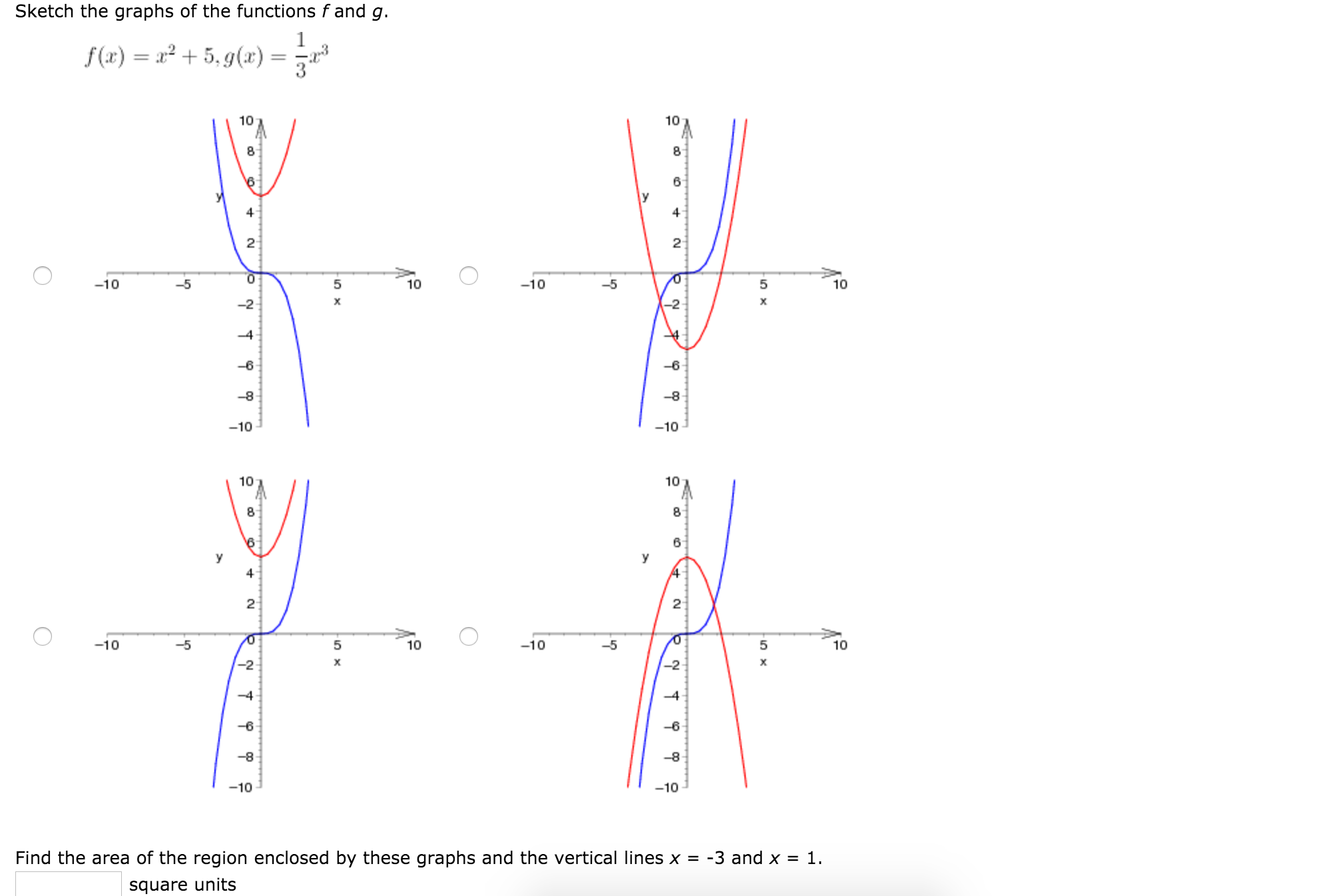



Solved Sketch The Graphs Of The Functions F And G F X Chegg Com
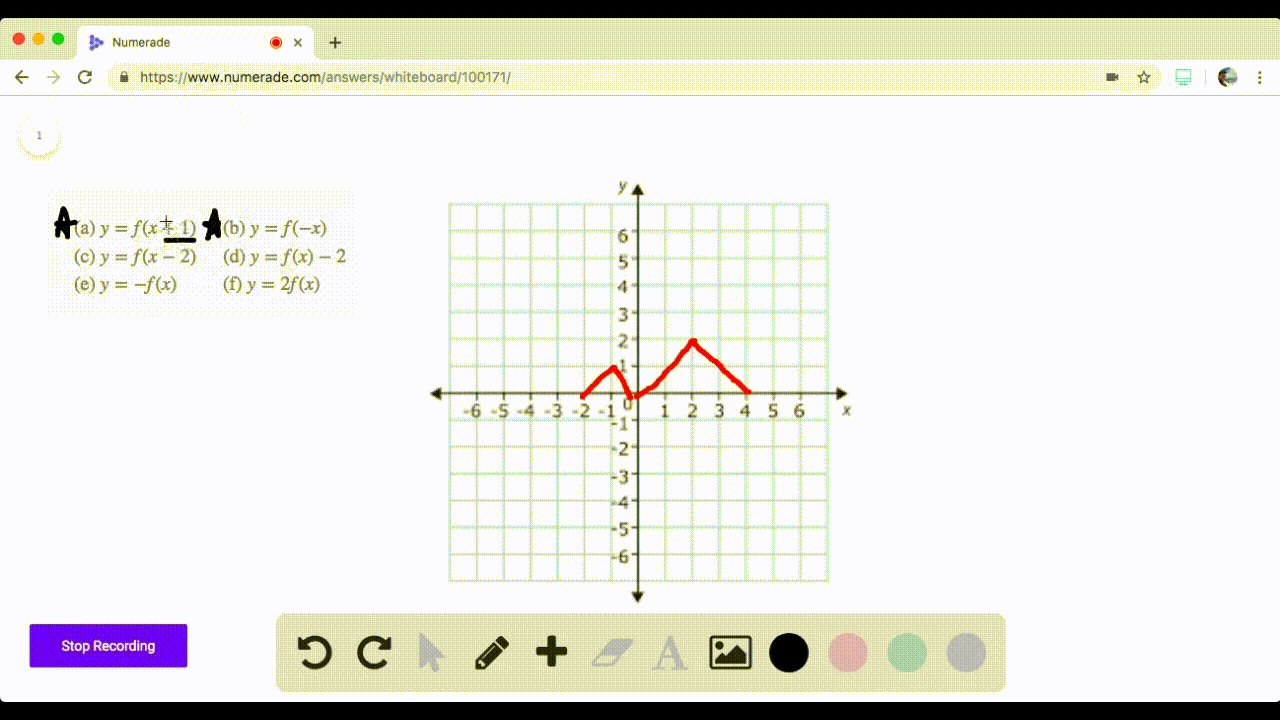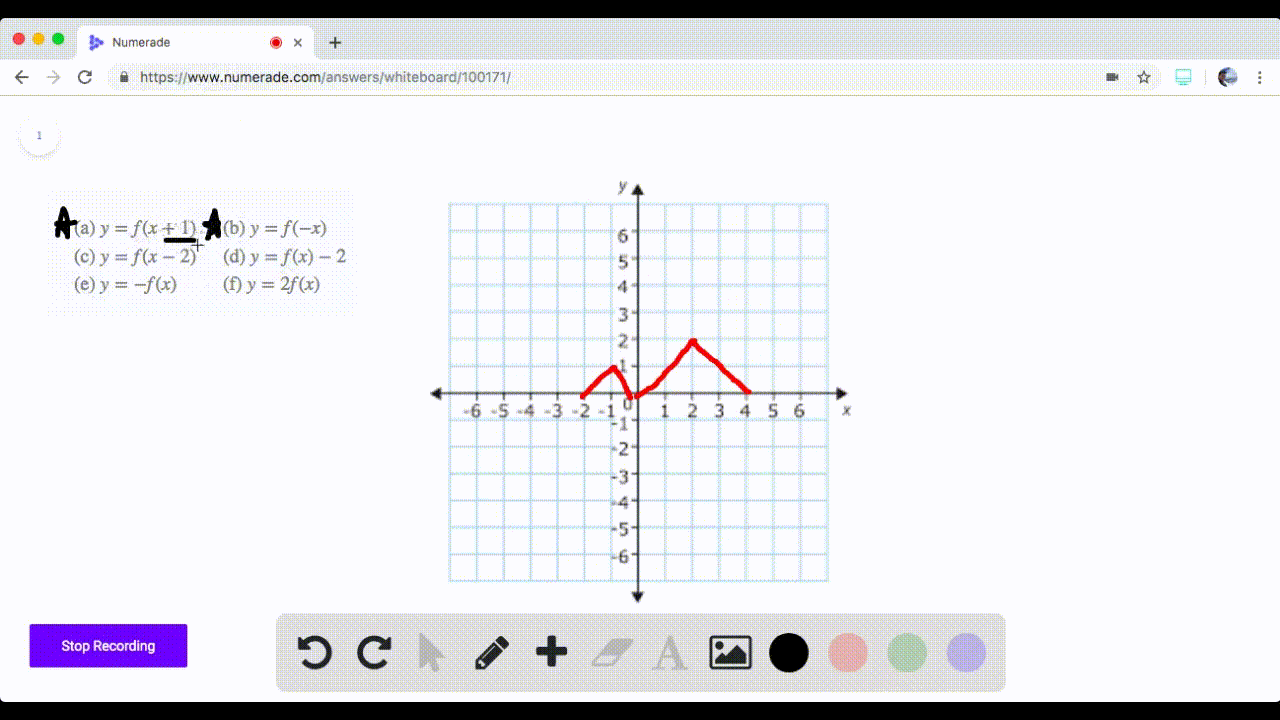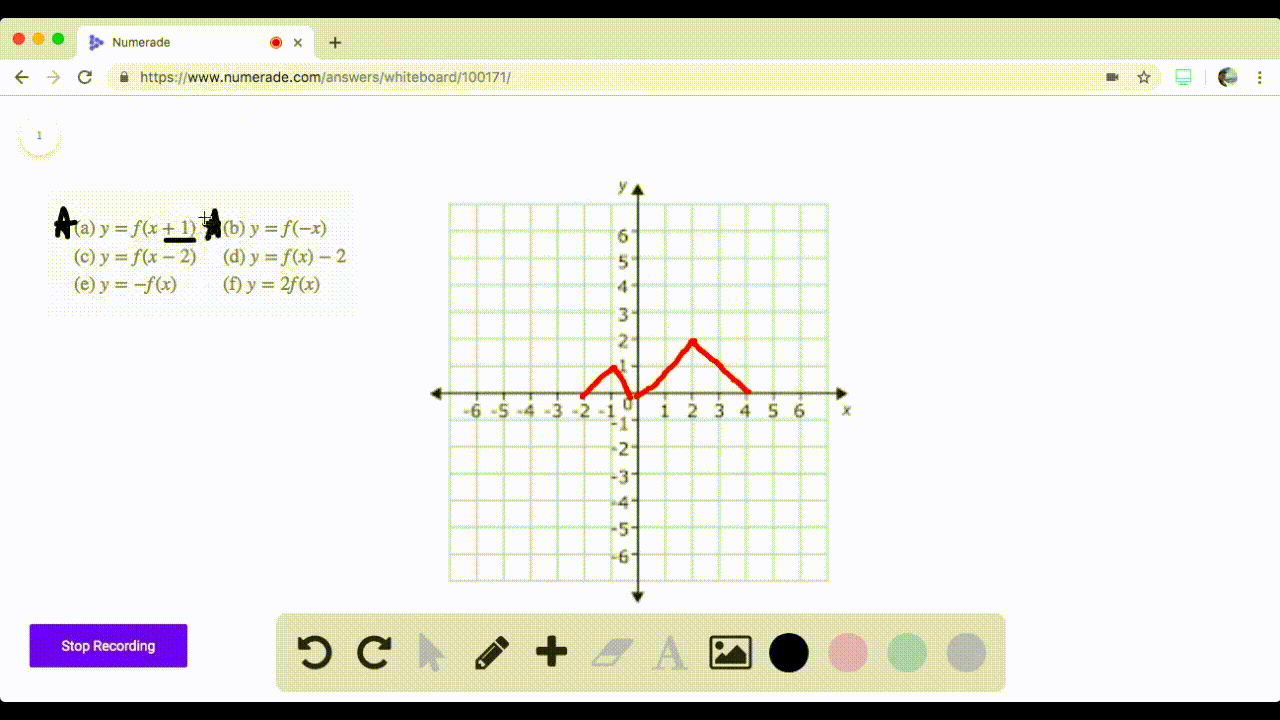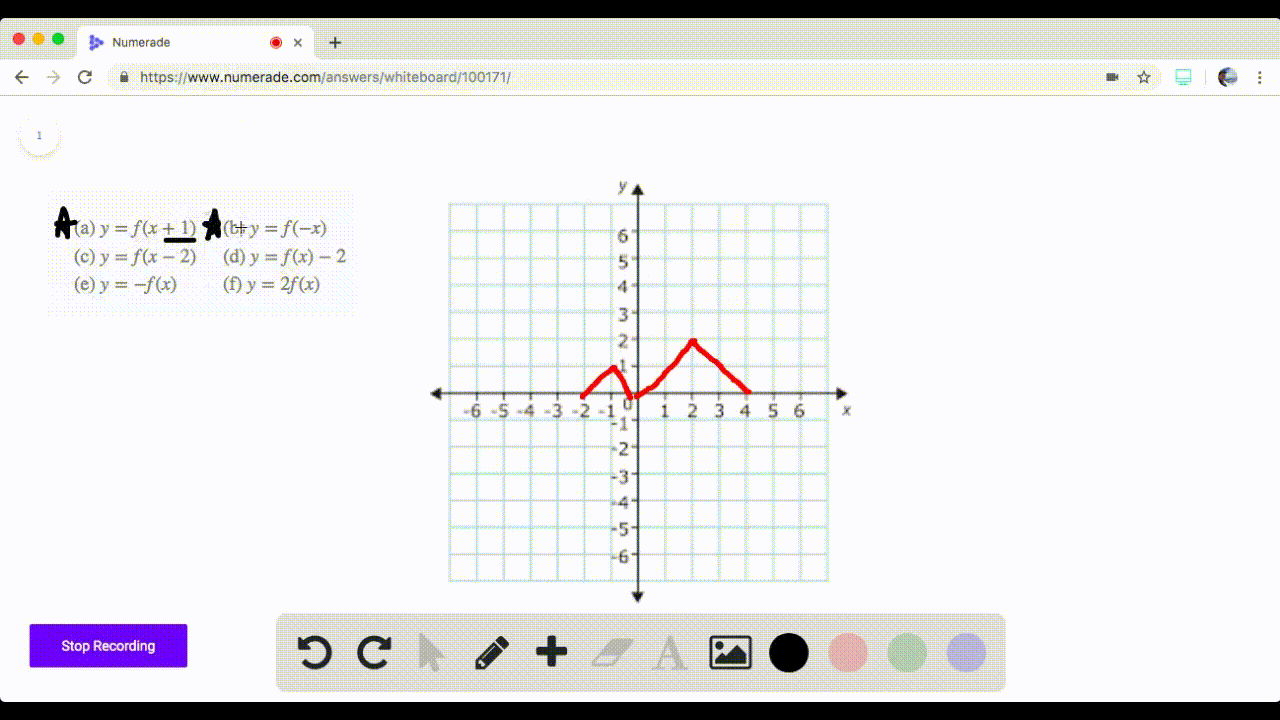



Solved 71 74 Graphing Transformations The Graph
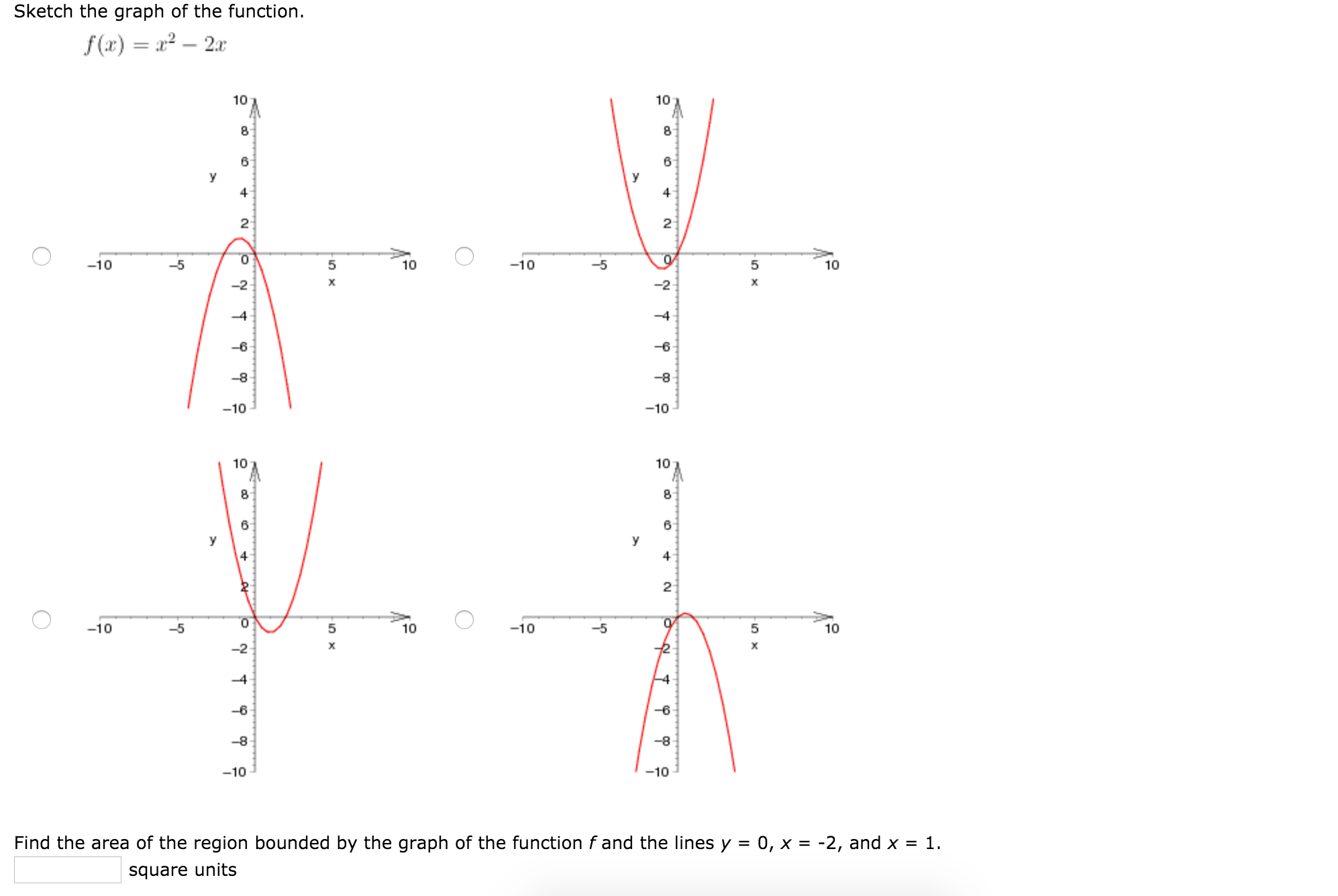



Sketch The Graph Of The Function F X X2 2x Find Chegg Com



Free Essays Homework Help Flashcards Research Papers Book Reports Term Papers History Science Politics



0 件のコメント:
コメントを投稿